[Dacon] COVID-19 Modeling
COVID-19 Modeling
Spatio variation of COVID-19 spread focusing on infection Hotspot
이번 포스팅에서는 앞 서 EDA를 진행한 데이터들을 바탕으로 Modeling에 들어가보겠습니다.
본 게시글은 연세대학교 응용통계학과 대학원 “시공간 자료분석 (박재우 교수님)” 수업의 파이널 프로젝트였음을 미리 밝힙니다.
Objective
저는 EDA를 진행하던 중 확진자들의 감염 경로에서 다양한 집단 발병지에 주목했습니다. 20년 초 신천지 case가 그러했듯이, 하나의 집단 발병지역이 발생한 후에 그 주변 지역으로 확진자 전파의 효과가 크며 이를 예측한다면 COVID-19 대처에 유용할 것이라고 생각했습니다. 따라서 집단 발병지역을 기준으로 COVID-19가 주변 지역으로 퍼져나가는 것을 예측하는 것이 본 분석의 목적입니다.
우선은 집단 발병으로 인한 확진자 발생 현상이 뚜렷했던 대구/경북 지역을 중심으로 모델을 fitting한 뒤 전국으로 확대해보겠습니다. 아래 그림은 대구/경북 지역의 집단 발병 지역을 나타낸 plot입니다.
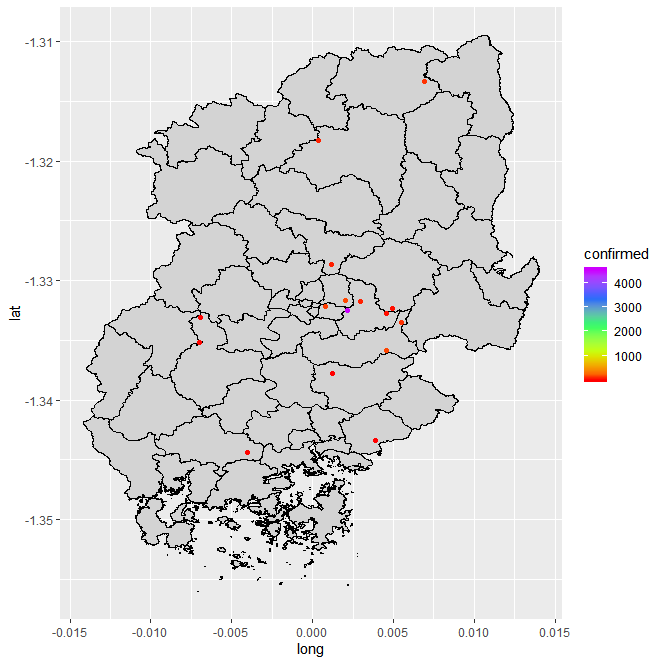
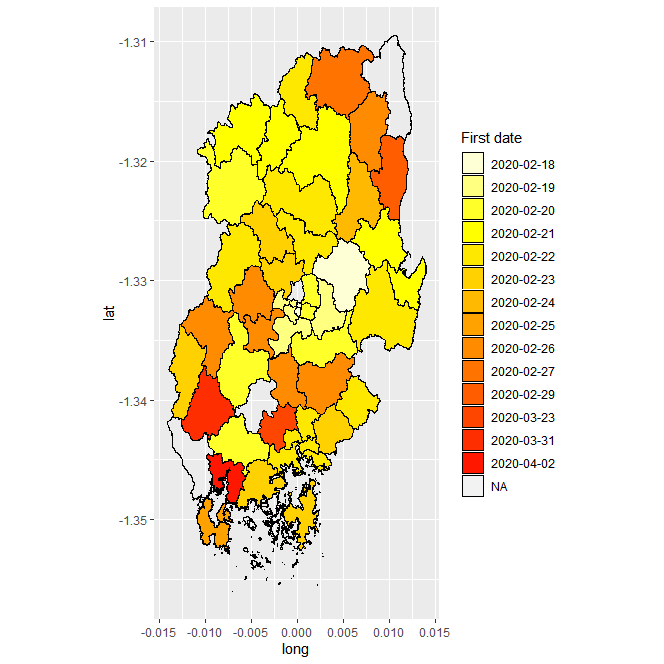
위의 16개의 집단 발병 지역(ex. 신천지 교회, 청도 대남병원 등)을 기준으로 주변 지역의 전파를 예측해보겠습니다. 전파 추세를 살펴볼 때는 각 지역의 첫 확진자 발생 날짜를 기준으로 살펴보고자 합니다. 최종적으로 다음의 plot을 예측하는 것이 목표입니다.
Methodology
Predict the date
저는 분석을 위해 Bayesian inference를 통한 Hierarchical SGLMM을 이용하고자 합니다. 일단 예측하고자 하는 첫 확진자 발생 날짜를 $Y$라고 한다면 우리의 데이터가 point-reference 데이터이므로 다음과 같이 표현이 가능합니다.
\[\begin{gathered} \mathbf{Y(s)} = \{Y(s_1), Y(s_2), ... , Y(s_n)\}, s_i \in \Re^2\\\textit{where } \{s_1, s_2, ... , s_n\} \textit{are locations} \end{gathered}\]이러한 $\mathbf{Y(s)}$를 예측하기 위해 Gaussian process를 이용한 Kriging으로 일종의 선형식을 fitting합니다. 사용되는 항으로는 첫 째로 $\mathbf{Y(s)}$의 추세를 예측할 mean function, 둘 째로 spatial correlation effect를 반영해주는 term, 마지막으로 불규칙성을 반영할 nugget term이 존재합니다.
여기서 mean function을 예측할 때 3가지 변수가 사용되며 각각 위도, 경도, 집단 발병지의 확진자 수가 사용됩니다. 집단 발병지의 확진자 수를 세부 변수로 넣는 이유는 집단 발병의 심각성에 따라 확진자 전파에 weight를 다르게 부여하고 싶었기 때문입니다.
\[\begin{gathered} \mathbf{Y(s)} = \mathbf{\mu(s)} + \mathbf{w(s)}+\mathbf{\epsilon(s)}\\ \textit{where } \mathbf{\mu(s)}=\mathbf{\beta_0}+\mathbf{\beta_1 X_1} +\mathbf{\beta_2 X_2}+\mathbf{\beta_3 X_3},\\ \mathbf{w(s)} \sim GP(0, K(\cdot)) \textit{ with Matern covariance},\\ \mathbf{\epsilon(s)} \sim N(0, \tau^2) \end{gathered}\]위 식에서는 총 4가지의 변수가 fitting되어야 합니다. 먼저 mean function에서 사용한 변수들에 대한 $\beta$, spatial correlation 반영을 위해 사용한 Matern covariance 내부의 변수 $\sigma^2$, $\phi$, 불규칙 nugget term의 변수 $\tau^2$가 바로 그 것입니다. 우리는 Hierarchical MCMC를 통해서 각 변수들을 estimate해보겠습니다. 먼저 MCMC를 위해 각 변수들에 대한 prior를 줍니다. 최대한 non-informative하면서 conjugate한 prior로 선정합니다.
\[\begin{gathered} \mathbf{\theta} = (\beta_0, \beta_1, \beta_2, \beta_3, \sigma^2, \phi, \tau^2)\\ \textit{where priors are }\\ p(\mathbf{\beta}) \sim N(m_{\beta}, V_{\beta})\\ p(\sigma^2) \sim IG(a_{\sigma^2},b_{\sigma^2})\\ p(\phi) \sim U(a_{\phi},b_{\phi})\\ p(\tau^2) \sim IG(a_{\tau^2},b_{\tau^2}) \end{gathered}\]이 후 20만번의 iteration을 통해서 변수들의 estimate을 구합니다.
\[\begin{gathered} \mathbf{\hat{\theta}} = \dfrac{1}{n}\sum_{i=1}^{n}\mathbf{\theta_i} \textit{, where } n=200,000 \end{gathered}\](MCMC의 수렴 결과는 다음과 같습니다.)
Predict the direction
위의 과정으로 $\mathbf{Y(s)}$를 fitting한다면 일종의 estimate된 함수 공간을 갖게 됩니다. 이 때 집단 발병 point를 기준으로 공간의 gradient의 derivative $\nabla\mathbf{\hat{Y(s)}}$를 구할 수 있습니다. 이렇게 구해진 gradient derivative를 기준으로 COVID-19의 전파에 대한 dominant effect direction을 예상해볼 수 있으며 이의 length, $\mid\nabla\mathbf{\hat{Y}(s)}\mid$를 이용하여 전파의 범위까지 예측할 수 있습니다.
Result
최종적으로 예측된 결과를 plot으로 그려주면 다음과 같습니다.
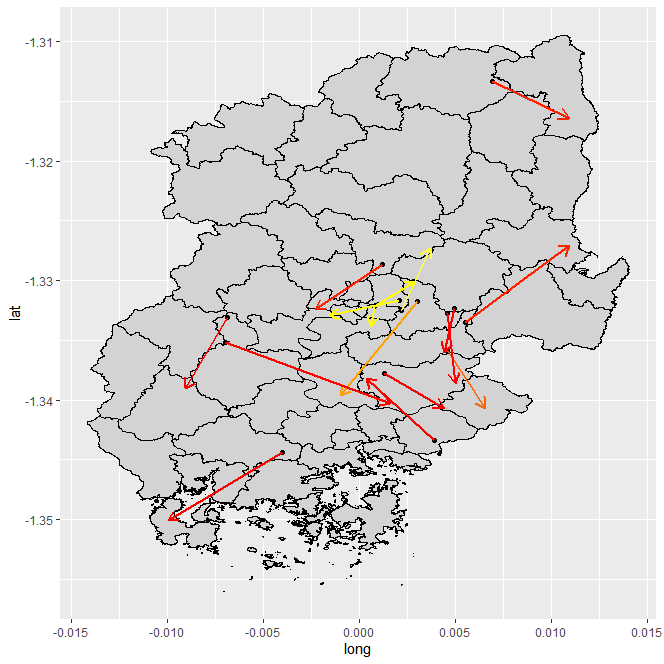
집단 발병 지역을 기준으로 전파 범위에 대한 예측이 화살표로 표시되어 있습니다. 이 예측이 실제로 정확한 지 글 초반에 target map에 중첩하여 표현해보겠습니다.
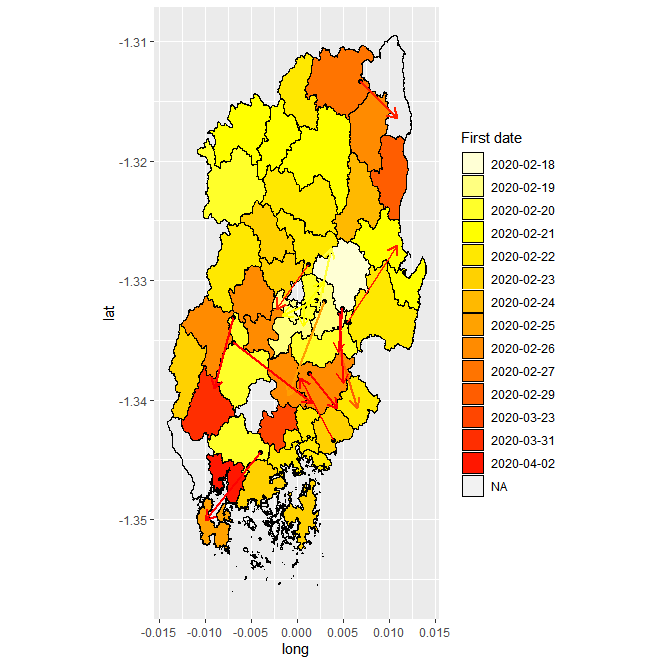
화살표의 방향과 색깔이 지역별 색깔과 비슷할수록 정확한 분석입니다. 대체로 첫 확진자 날짜와 비슷하게 예측하는 것을 확인할 수 있습니다.
마지막으로 예측 범위를 전국으로 확대해보겠습니다.
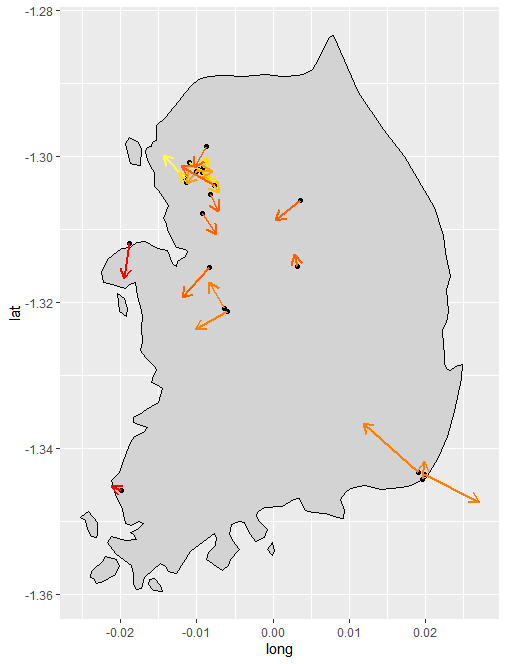
대구/경북 지역을 제외한 전국의 집단 발병지를 중심으로 전파 범위를 예측한 결과입니다. 범위 확장에 따라 본 분석의 두 가지 한계점이 드러납니다. 먼저 첫 번째로 분석 대상 자료가 point-reference 데이터이기 때문에 강원도와 같이 집단 발병 point가 없다면 예측이 어렵습니다. 또한 부산 지역의 집단 발병지에서 남해 지역으로 화살표가 뻗어나가는 것을 볼 수 있는데 이는 육지에 대한 정보가 없기 때문입니다. 따라서 model fitting 단계에서 사람들이 거주하는 지역에 대한 boundary를 넣어주어야 보다 정확한 분석이 가능할 것입니다.
