[Paper review] Anomaly Transformer

시계열 데이터의 이상치 탐색 방법론으로서 Transformer 매커니즘을 활용한 Anomaly Transformer에 대해 리뷰해보겠습니다. ICLR 2022 의 spotlight 논문이라고 하네요!

Xu, Jiehui, et al. “Anomaly transformer: Time series anomaly detection with association discrepancy.” arXiv preprint arXiv:2110.02642 (2021)

(본 리뷰의 모든 수식과 그림은 원 논문을 참고했습니다.)

Idea

Anomaly Transformer는 이름에서 알 수 있듯이 Transformer를 활용하여 시계열 데이터에서의 Anomaly detection을 잘 해보자는 목적을 가지고 있습니다. 이상점을 탐색하는 방법으로는 reconstruction based 방법을 사용하고 있습니다. Reconstruction based 방식이란 주어진 train 시계열 데이터의 패턴을 통해 정상 시계열 패턴을 잘 재구축 하도록 모형을 학습시킵니다. (이 때 label이 따로 필요 없기 때문에 unsupervised learning입니다.) 추후에 test set이 들어왔을 때, 모형이 재구축(reconstruction)한 시계열 패턴과의 비교를 통해 그 차이가 큰 (anomaly score가 큰) 지점을 이상점으로 탐색하는 방법론입니다. 이 때, 정상 시계열 패턴을 잘 학습하도록 해주기 위해 Transformer를 활용합니다. Self-attention을 이상점 탐지에 특화되게 바꾼 Anomaly-attention을 제안하였습니다. 그럼 Anomaly Transformer에 대해 본격적으로 알아보도록 하겠습니다.

Anomaly Transformer

Anomaly Transformer의 architecture는 다음과 같습니다.

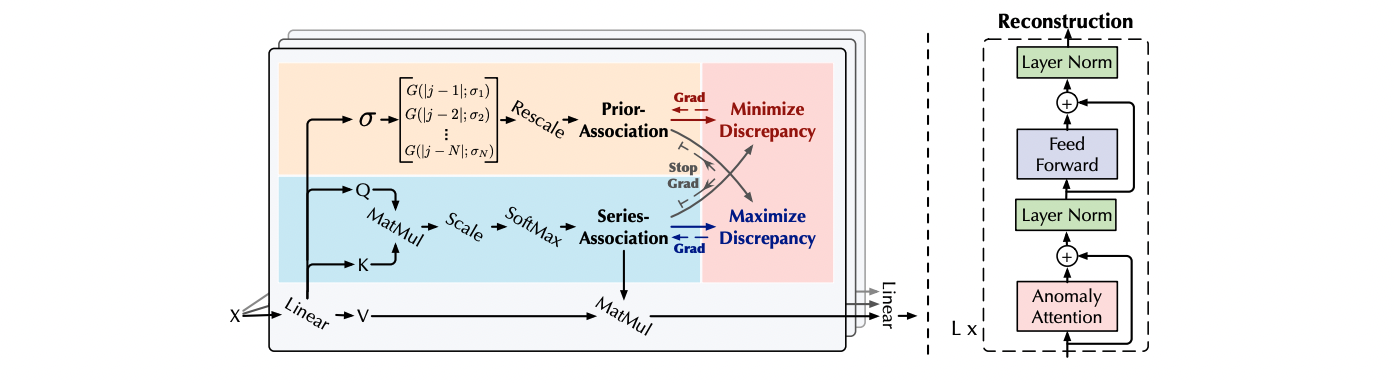
Anomaly Transformer architecture

Input embedding $X_{0}$가 들어오면 크게 Anomaly Attenion layer와 Feed Forward layer를 L번 반복 수행하며 input time series의 pattern을 학습하게 됩니다. 이후 이 학습된 정보를 가지고 가장 보편적인 pattern의 reconstruction data를 산출하는데요! 이 구조에서 가장 주목해야 하고, Anomaly transformer가 높은 성능을 가지는 이유는 단연 Anomaly attention일 것입니다.

Anomaly Attention

Anomaly attention은 기본적인 attention을 가지고 저자들이 time series anomaly detection에 맞게 매커니즘을 조금 수정한 형태입니다. 가장 큰 부분은 attention 내부를 Prior-Association과 Series-Association의 두 가지로 나누었다는 것입니다.

\[Prior-Association: P = \frac{1}{\sqrt{2 \pi}\sigma_i} exp(-\frac{(|j-i|)^2}{2\sigma^2_i}), i,j\in {1, ..., N}\] \[Series-Association: S = Softmax(\frac{QK^T}{\sqrt{d_{model}}})\]

먼저 prior association은 이름에서 알 수 있듯이, 모형에서 사용하는 Gaussian kernel의 시그마를 학습합니다. Gaussian Kernel은 attention의 Query, Key를 학습할 때 영향을 줍니다. 커널을 통해 다양한 패턴의 시계열 자료에 적용할 수 있다고 저자는 설명하고 있습니다. Series asssociation은 Query와 Key를 학습하는 부분입니다. 저자들은 이 두 association을 통해서(정확히는 prior association) 시계열 자료를 point-wise가 아닌, temporal dependency를 학습할 수 있다고 설명합니다. Gaussian Kernel의 $\sigma$를 통해서 인접한 time point에 더 큰 가중치를 줄 수 있다는 것이지요.

Association Discrepancy

Association Discrepancy는 앞서 살펴본 prior association과 series association간의 차이를 계산하는 것입니다. 차이를 계산하는 방법은 KL divergence를 활용하였으며, KL divergence의 assymetric한 점을 보완하기 위해 순서를 바꿔가며 계산한 평균을 사용하였습니다. Association Discrepancy는 Loss function의 한 term으로 포함되며 가중치를 업데이트 하는데 사용하기도 하고 추후 anomaly score를 계산하는 데에도 사용됩니다.

\[AssDis(P,S; X) = \frac{1}{L} \sum^L_{l=1}(KL(P^l_i||S^l_i) + KL(S^l_i||P^l_i))\] \[where\,\, i=1,...,N\]

Mini Max Association Learning

저자들은 Attention 내부에 prior & series association 두 개의 term이 있는 만큼 이를 활용하여 Loss function을 병렬적으로 구성하는 mini max learning strategy를 제안합니다. 우선 Anomaly transformer에서 사용하는 Loss function은 다음과 같습니다.

\[L_{total}(\hat{X}, P, S, \lambda; X) = (||X-\hat{X}||)^2_F - \lambda \cdot ||AssDis(P, S; X)||\]

수식을 보면 $\lambda$ term에 의해 Association discrepancy가 조절됨을 알 수 있습니다. $\lambda$가 0보다 크면 모형은 association discrepancy를 더 크게 만드는 방향으로 학습이 진행되며, 0보다 작으면 반대로 작게 만드는 방향으로 학습이 진행됩니다. 이 개념을 활용한 것이 바로 Mini max Strategy 입니다.

Mini max는 말 그대로 Minimize phase, Maxmize phase 두 부분으로 나누어 Loss function을 다르게 적용하는 것입니다.

\[Minimize: L_{Total}(\hat{X}, P, S_{detach}, -\lambda; X)\] \[Maximize: L_{Total}(\hat{X}, P_{detach}, S, \lambda; X)\]

수식에서 알 수 있듯이, Minimize phase때는 Prior association을 학습하고, Maximize phase 때는 Series association을 학습합니다. 이 때, $\lambda$의 부호에 따라 학습의 방향이 달라지는 것입니다. 논문의 그림을 보면 좀 더 이해하기 쉽습니다.

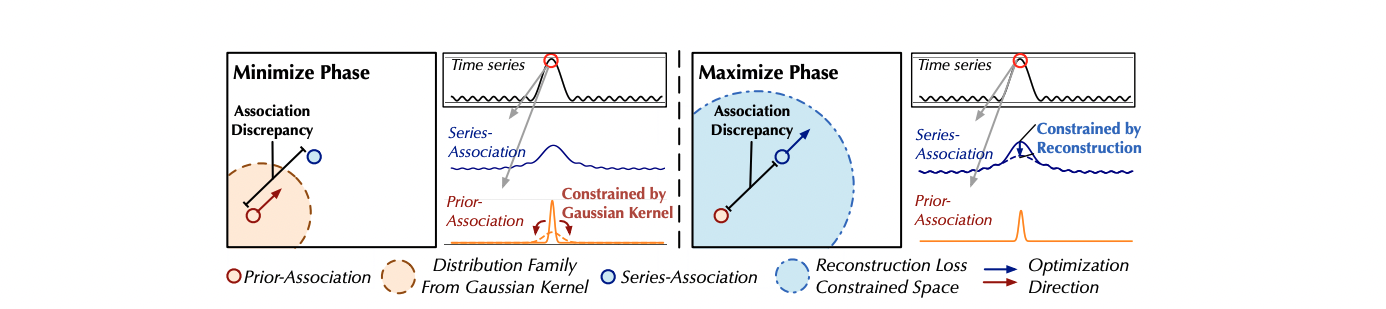
먼저 왼편의 Minimize phase를 보면 Loss function의 $\lambda$ 가 0보다 작기 때문에, association discrepancy, 즉, Prior association과 Series association의 차이를 작게 만들어주는 방향으로 학습됩니다. 이를 해석해보면 Gausian prior의 $\sigma$를 주어진 time series pattern에 가장 적절하게 tuning시켜주는 작업이라고도 할 수 있을 것 같습니다.

중요한 것은 오른쪽의 Maxmize phase인데요. 사실상 이 부분을 통해 모형이 Anomaly를 찾는다고도 할 수 있겠습니다. 앞 서와는 달리 $\lambda$가 0보다 크므로 두 association간의 차이가 커지도록 학습을 하게 됩니다. 따라서 그림에서와 같이 시계열 내에서 anomaly pattern을 보이는 시점에서의 경우 Association discrepancy가 더 커지도록 (벌어지도록) 해줍니다.

Association-based Anomaly Criterion

\[Anomaly Score(X) = Softmax(-AssDis(P, S; X)) \odot (||X_{i, :}-\hat{X}_{i, :}||)^2\] \[where\,\, i=1,...,N\]

Anomaly Transformer가 Anomaly들을 detect하는 score입니다. 기본적으로 reconstruction error를 기반으로 탐색을 하지만, 본 모형만의 Association discrepancy term이 추가되어 상호 협력적으로 이상점을 탐지하는 것을 확인할 수 있습니다. 이를 통해 성능을 더욱 향상시킬 수 있다고 저자들은 설명합니다.

Experiments

본 논문의 가장 경악(?)스러운 부분은 바로 이 실험 결과 부분입니다. 저자들은 Anomaly transformer의 탐지 성능을 실험하기 위해 15개의 이상치 탐색 관련 모형들과 비교하였으며 이를 위해 5개의 서로 다른 시계열 데이터들을 사용했습니다. 그 결과는 다음과 같습니다.

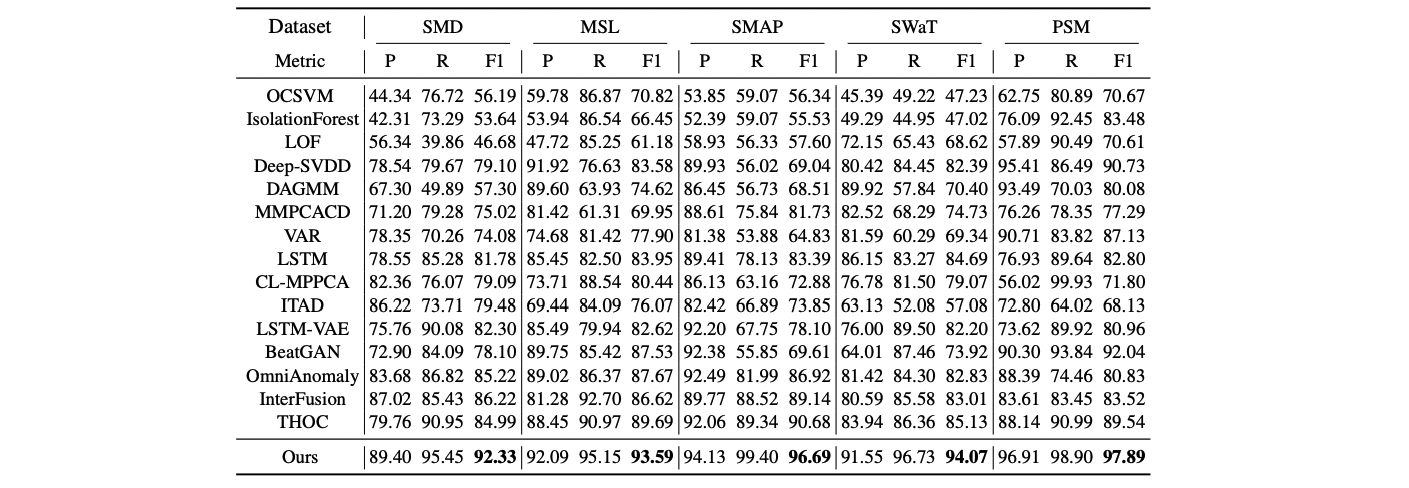
전체 5개의 데이터 셋에서 저 수많은 모형들 중 Anomaly transformer가 압도적인 SOTA를 달성함을 확인할 수 있습니다. 심지어 모든 데이터에서 F1 score가 90을 넘는 기염을 토하는데요. 이를 그림으로 직관적으로 확인해보아도 놀랍습니다.

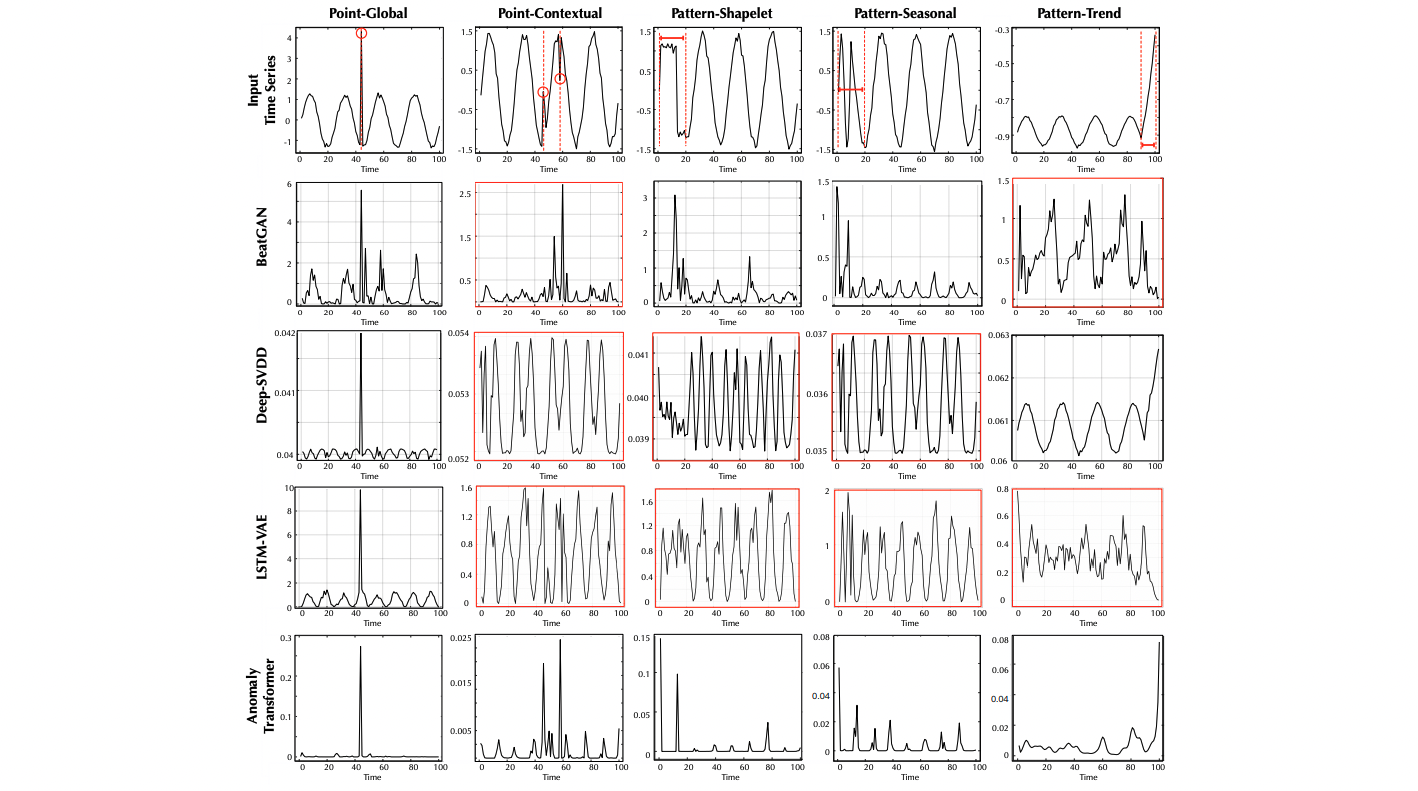
가장 윗 줄이 input으로 들어간 original 시계열 자료의 모습이고 그 아래로 각 모형이 계산한 anomaly score들이 나타나 있습니다. 원 자료에서 빨간색으로 표시되어 있는 이상점 부분에서의 score가 높아야만 모형이 이상치로 탐색할 수 있습니다. 그림을 살펴보면 맨 아래쪽 행에 있는 Anomaly transformer는 모든 이상점 구간에서 정확히 score가 높아져, 이상치를 잘 판별하고 있습니다. 이에 비해 다른 모형들은 (특히 point-contextual 이상 패턴에서) 이상치를 탐지하는 데 어려움을 보이는 case가 존재함을 확인할 수 있습니다.

지금까지 Anomaly transformer에 대해 알아보았습니다. 기존 언어 모형에서 활용되던 Transformer를 시계열에도 적용한 점이 인상깊었습니다. Transformer의 압도적 성능 덕분인지, Association discrepancy등 저자들이 새로 제시한 아이디어 덕분인지 (아마 종합적으로 작용했을 것 같네요) 어마어마한 SOTA모형이 탄생한 것 같아 흥미롭습니다!

[Review] Anomaly Transformer