[Review] SHAP

ML/DL 모형들이 널리 쓰여지면서 모형의 결과에 대해 해석이 가능한 지에 대한 연구도 활발히 진행되고 있습니다. 주로 Feature Importance나 LIME과 같이 주로 변수들이 모형에 얼마나 영향을 미쳤는지를 파악하는 형태로 해석하게 되는데요! 이런 방법론 중 가장 이론적 뒷받침이 탄탄하다고 알려진 SHAP에 대해 공부한 바를 간단히 정리해보고자 합니다.

SHAP이란?

SHAP(SHapley Additive exPlanation)은 Shapley value를 활용하여 모형의 결과에 대해서 각 특성(변수)의 기여도가 어느 정도인지 계산하는 방법론입니다. 이 기여도를 통해서 어떤 변수가 모형의 결정에 얼마나 영향을 미쳤는지 확인할 수 있고, 이를 통해 모형을 해석하는 것이지요. 방법론의 목적이나 아이디어는 Permutation기반의 feature importance와 차이가 없습니다만, SHAP의 경우가 좀 더 이론적 배경이 탄탄하며, 변수의 기여도를 계산할 때 조건부 확률의 개념을 적용함으로써 변수 간의 상관관계에 영향을 덜 받는다는 장점이 있습니다. SHAP의 저자인 Lunberg와 Lee는 kernel SHAP과 Tree SHAP의 두 방법을 제안했습니다. 이 방법론들을 알아보기 전에 먼저 Shapley value에 대해서 간단히 확인해보겠습니다.

Shapley Value

Shapley value는 게임 이론에서 파생된 개념이라고 합니다. 어떤 결과를 위해 참여자들(players)들이 얼마나 기여했는지를 계산하는 것이라고 하는데요. XAI에서는 이 개념이 각 변수들을 참여자들로 보고 모형의 결과를 나타내기 위해 변수들이 얼마나 기여했는지를 계산하는 방식으로 쓰여집니다. 구체적으로 어떤 개념인지 유명한 사례를 통해 살펴보겠습니다.

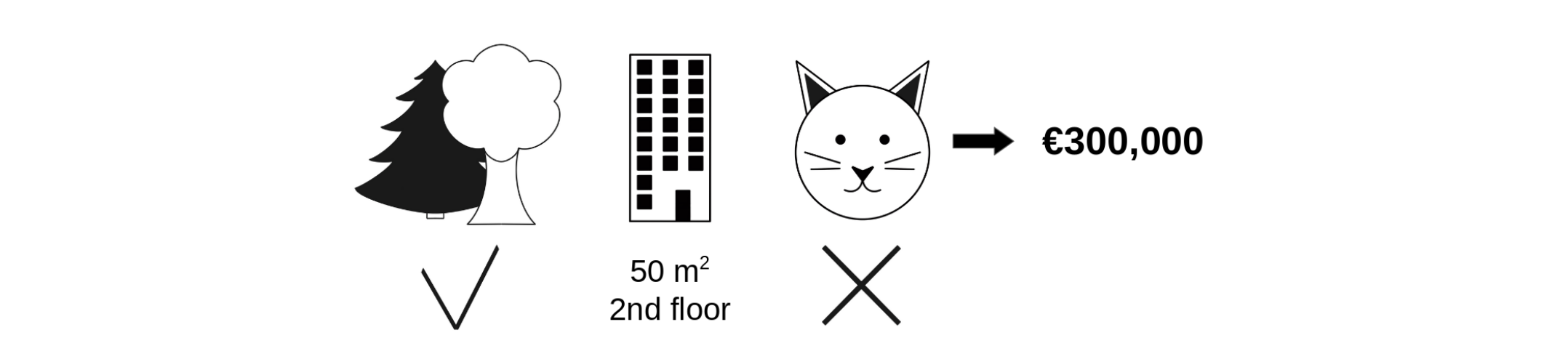
우리의 모형이 어떤 아파트의 가격을 30만 유로라고 예측했다고 가정합시다. 이 때 모형 안에 있는 변수는 3가지입니다. 1. 근처에 공원이 있으며, 2. 50제곱미터 크기의 2층이고, 3. 고양이 출입이 금지되는 곳이라는 것입니다. 이 세 가지 정보 중 고양이 출입이 금지되었다는 변수가 가지는 기여도에 대해 확인해보고 싶습니다.

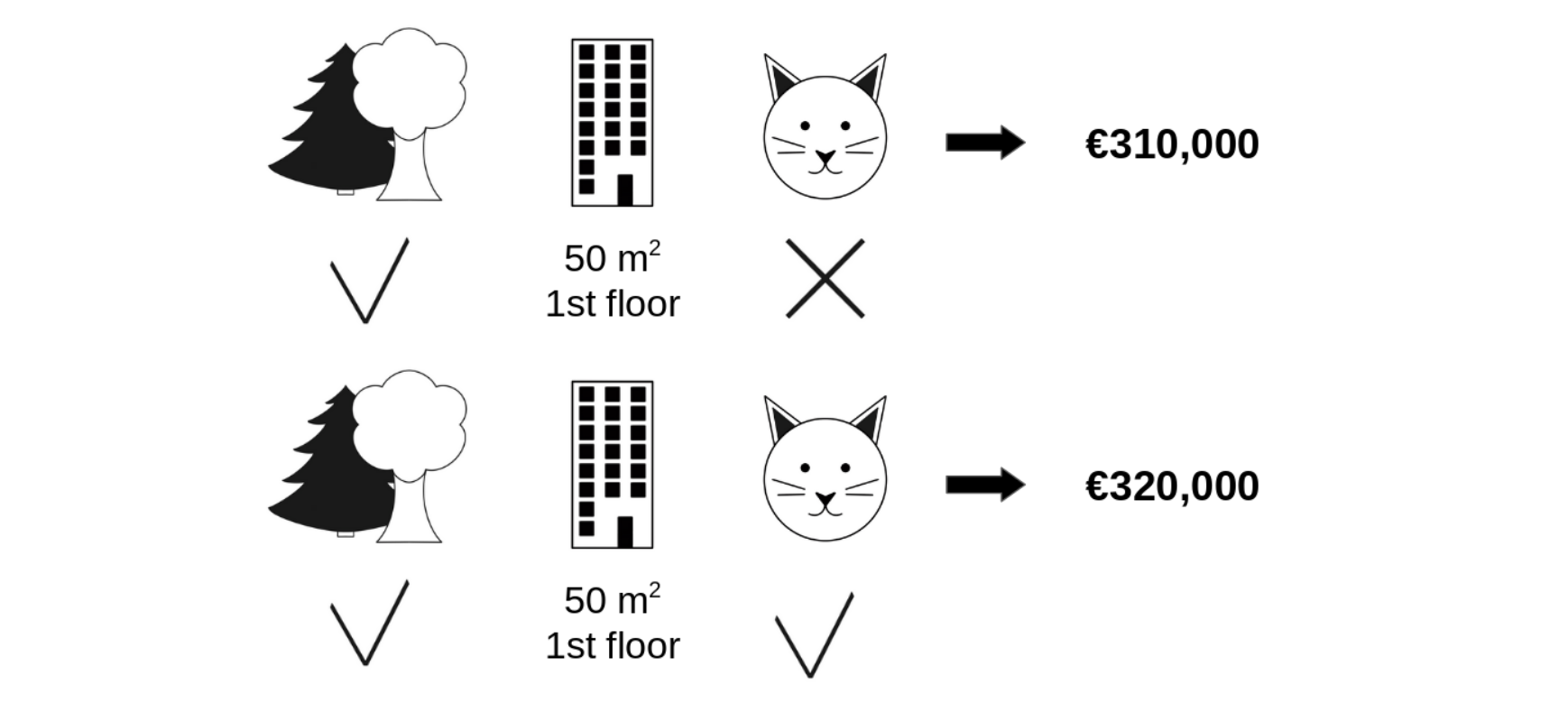
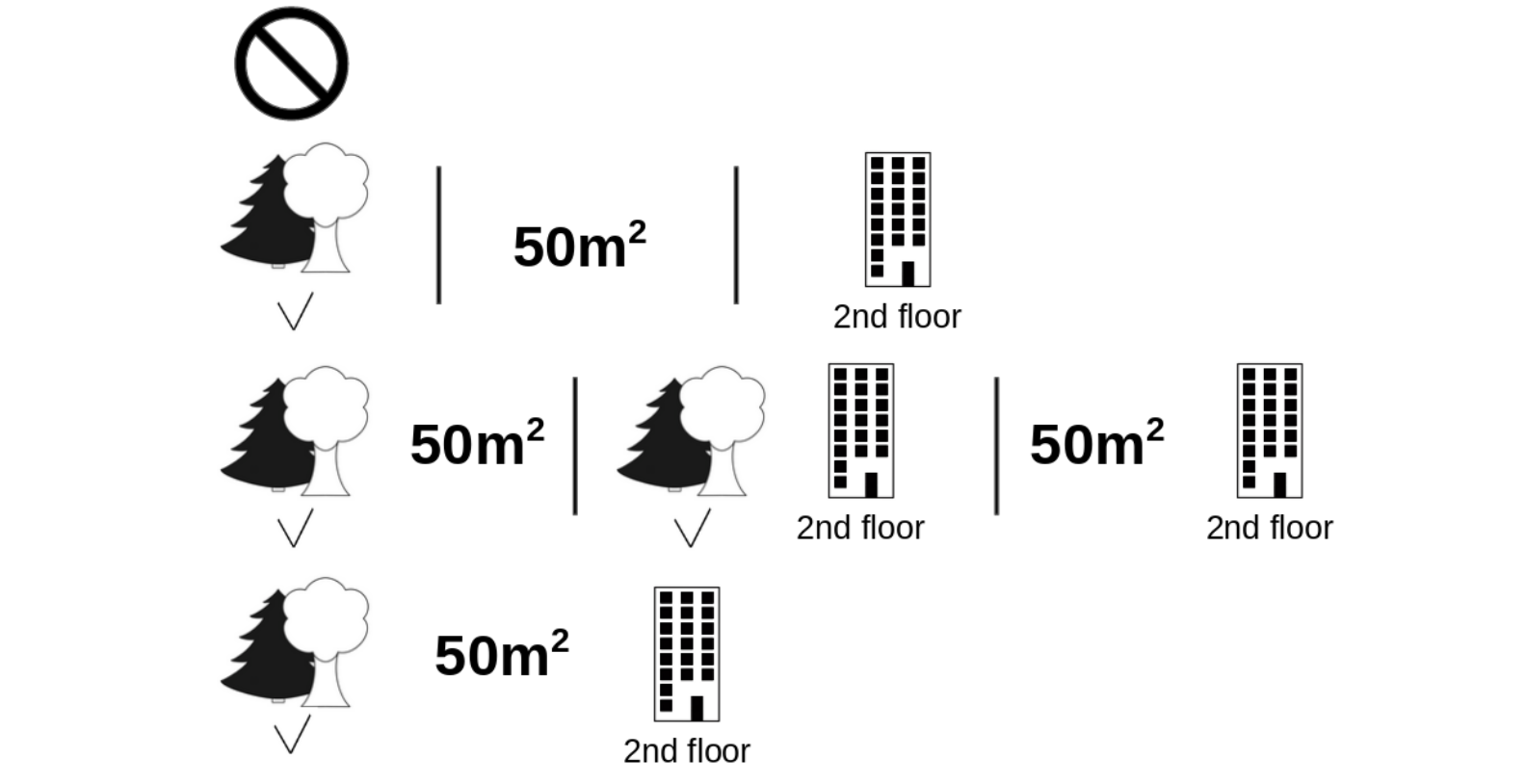
위 그림처럼 고양이 다른 변수는 동일하게 고정한 채, 고양이 출입 가능 여부만 바꿔서 계산해보면 고양이 출입에 대한 기여도를 확인할 수 있습니다. 모형은 고양이 출입이 허용되면 집 값이 1만 유로 더 비싸질 것이라고 예측하는 것으로 보아 고양이 출입이 집 값에 + 영향을 미친다고 보고 있군요. Shapley value는 여기서 그치지 않고 다른 두 변수의 가능한 모든 경우의 수 조합으로 확장하여 고양이 출입 변수에 대한 기여도를 계산합니다. 이를 통해 가장 객관적인 고양이 출입 변수에 대한 기여도를 확인할 수 있게 되는 것입니다. 모든 경우의 수는 $2^3=8$ 가지 입니다.

Kernel SHAP

앞서 SHAP은 Shapley value를 활용하여 변수 기여도를 계산한다고 말씀드렸습니다. 그 중에서 가장 먼저 나온 Kernel SHAP의 매커니즘을 살펴보겠습니다.

Sample coalitions $ z_k \in ${0,1}$^M, k \in ${1,…,K}$ $ (1=feature present in coalition, 0=feature absent)
Get prediction for each $z_k$ by first converting $z_k$ to the original feature space and then applying model $g$ : $g(h_x(z_k))$
Compute weight for each $z_k$ with the SHAP kernel
Fit weigted linear model
Return Shapley value $\phi_k$, the coefficients from the linear model

복잡해보이지만 하나씩 살펴보면 아이디어는 어렵지 않습니다. 우선 $z_k$부터 이해해보면 변수가 있으면 1, 없으면 0으로 표시하는 조합들입니다. NLP에서의 one-hot embedding과 똑같은 개념이라고 이해하면 될 것 같습니다. 이렇게 나타내는 이유는 위의 shapley value에서 살펴본 것처럼 변수의 존재 유무의 조합에 따라 변수 기여도를 계산하기 위해서 입니다.

2번을 보시면 $h_x$ 함수가 나옵니다. 이는 0,1로 구성되어 있는 $z_k$를 x와 유사하도록 mapping 시켜주는 일종의 장치입니다. 아래 그림을 살펴보시죠.

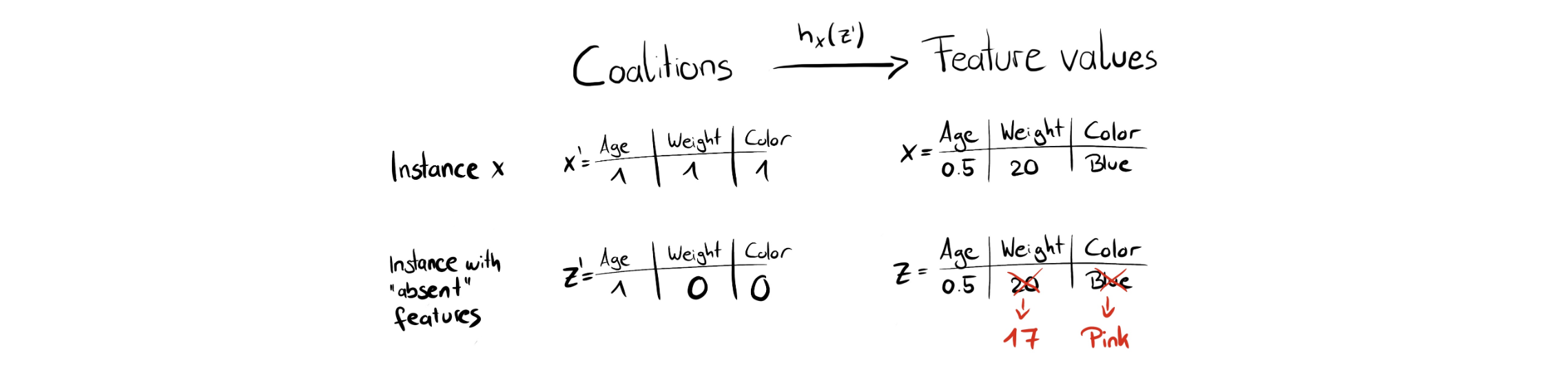
x를 살펴보시면 age, weight, color 세 가지 변수가 있고, 아래에는 그 중 age만 존재하는 조합 $z$에 대해 표현되어 있습니다. 이 때 이 $z$를 기존 $x$처럼 변환시켜주는 것이 $h_x$입니다. 그림에서는 각각 17과 pink로 대체하는 것을 볼 수 있는데요. 이는 데이터 셋 내의 다른 변수들을 랜덤으로 고릅니다. (랜덤으로 대체하는 이 부분 때문에 Kernel SHAP 또한 Permutation 기반 해석 방법과 동일한 문제를 갖는다고 합니다.)

이제 SHAP에 필요한 구성 요소들에 대해 알았으니 SHAP의 큰 아이디어를 정리해보겠습니다. SHAP에 대해 정리하던 중 이를 잘 표현한 블로그 내 그림이 있어 가져왔습니다.

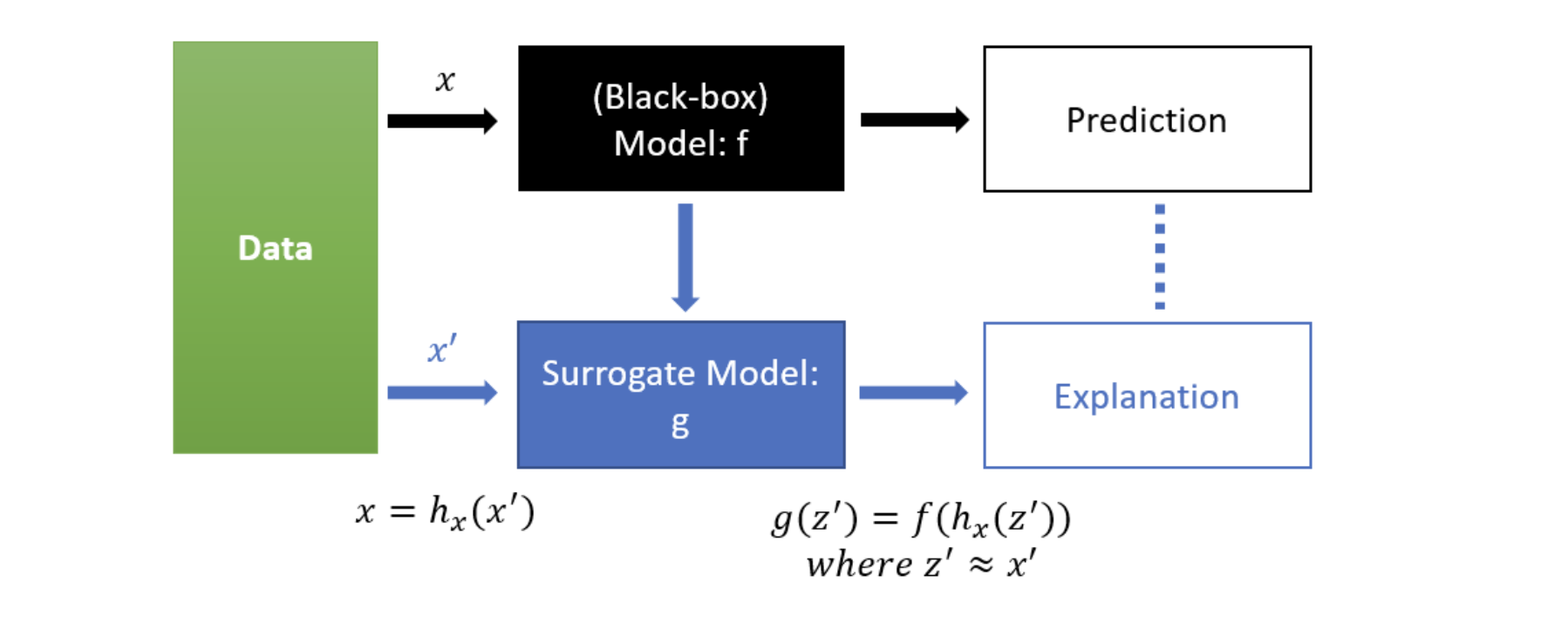
현재 우리가 해석하고 싶은 모형은 black box인 $f$입니다. 우리는 이 f를 가장 잘 설명하는 $g$라는 모형을 “새로” 추정하고자 합니다. $g$는 Shapley value를 계수로 하는 linear 모형이며, 마침내 이 계수 값을 통해 우리는 각 변수들의 기여도를 확인할 수 있습니다. 선형 회귀의 $\beta$를 해석하는 것과 동일하게 말이죠.

\[g(z) = \phi_0 + \sum^M_{j=1}\phi_j z_j\]

$g$를 학습하기 위한 Loss function은 아래와 같습니다. (아이디어만 확인하기 위함이므로 수식을 단순화 하였습니다. 실제로는 shapley kernel term이 가중치로 들어있습니다.)

\[L(f, g) = \sum[f(h_x(z))-g(z)]^2\]

SHAP의 활용

이렇게 SHAP의 이론은 복잡한 것 같지만 사실 실제 활용은 어렵지 않습니다. 파이썬이 알아서 다 해주니까요! ㅎㅎ

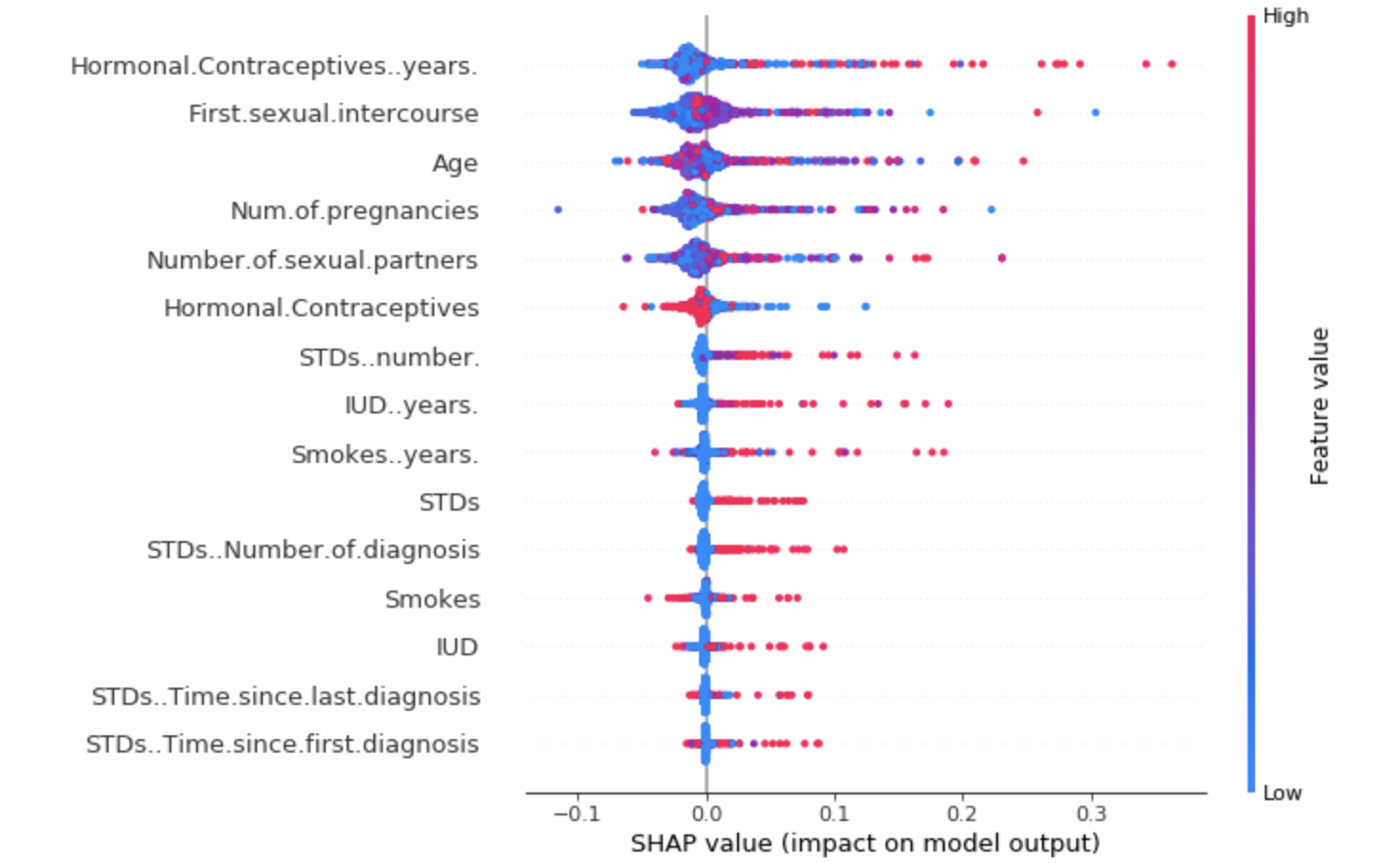
파이썬에서 SHAP 라이브러리를 통해 나온 결과입니다. 세로 축에는 모형이 사용하고 있는 변수들이 쭉 나열되고 가로 축에는 각 변수들의 SHAP value들이 표현됩니다. SHAP value의 절대값이 클수록 모형에 기여하는 영향이 큰 것입니다. 오른쪽 이중축에는 변수 자체의 값에 대해 표현되고 있는데요, 빨간 색일수록 큰 것이고 파랑색일수록 작은 값이라는 뜻입니다.

플랏을 해석해보자면, 먼저 맨 위의 변수인 Hormonal Contraceptives years를 살펴보면 Shap value가 음수인 부분에는 파란색 점이, 양수인 부분에는 빨간점이 비교적 많이 분포하는 것을 확인할 수 있습니다. 이를 해석해보면 이 변수의 값이 작을 수록 모형의 결과 값에는 -, 음의 영향을 미치는 것을 알 수 있고, 값이 클수록 모형에 + 영향을 미칩니다. 특히, 변수의 값이 클 때 비교적 모형에 많이 기여하는 것을 확인할 수 있네요!

SHAP이란?

Shapley Value

Kernel SHAP

SHAP의 활용

Reference