GloVe 이해하기!

이번 포스팅은 Word representation의 한 방법론인 GloVe에 대해서 알아보도록 하겠습니다.

GloVe는 Word embedding 방법 중 Distributed representation에 해당하는 방법론으로, 기존의 Word2Vec이나 LSA와 같은 알고리즘이 가지고 있던 한계점들을 보완하여 개발한 알고리즘입니다.

본 글에서는 GloVe가 기존 알고리즘에 비해 어떤 이 점을 갖는지, 어떤 프로세스를 거쳐 텍스트의 Distributed form을 찾게 되는 지 등에 대해 살펴보도록 하겠습니다.

Distributed Representation

Word representation 방법의 초기 모델은 WordNet이나 One-hot Vector 방법이 있습니다. 이 방법론들은 분석자가 미리 단어의 사전적 뜻을 정해두어 표현하거나, 단순 1,0 변환으로 표현하는 것입니다. 이는 비교적 직관적인 이해를 하기에 용이하나 단어의 분포적 특성을 파악하지 못하므로 단어들의 관계나 동명이의어 등을 쉽게 파악해내지 못합니다. 이에 보다 발전적인 방법론이 대두된 것이 Distributed Representation 방법입니다. Distributed Representation은 말뭉치(Corpus)를 기반으로 단어의 출현 빈도를 Word vector로 변환하여 학습하는 방법입니다. 이 전 방법론에 비해 단어의 관계를 표현하는것이 가능하며, 사람의 주관적 개입도 최소화할 수 있다는 장점을 가지고 있습니다. Distributed Representation의 대표적인 알고리즘으로는 Word2Vec과 LSA를 들 수 있습니다.(본 포스팅에서 다루는 GloVe도 포함됩니다.)

하지만 이러한 Word2Vec과 LSA에도 단점이 존재합니다. 먼저 Word2Vec의 경우 중심단어로부터 사용자가 지정한 window내에서만 관계를 파악하여 분석하기 때문에 Corpus 전체의 통계정보, 즉, Co-occurrence 정보를 반영하지 못하는 단점이 있습니다. 더하여 한 번에 하나의 계산만 수행하기 때문에 업데이트에 어려움이 있습니다. 다음으로 LSA의 경우 Corpus 전체의 Co-occurrence 정보는 모두 반영되는 대신, 단어 간 유사도나 관계에 대해서는 파악하기 어려운 단점을 가집니다.

GloVe는 이러한 단점들을 보완하여 발전시킨 방법론이라 할 수 있습니다. 즉, Corpus 전체의 Co-occurrecnce는 모두 반영하면서 단어간 유사도도 측정할 수 있는 방법론이라 할 수 있습니다.

How to do that? “Probability of Co-Occurrence”

위의 단점들을 해결하는 방법으로 GloVe 연구팀이 제시한 것이 바로 “동시등장확률(Probability of Co-occurrence)”입니다. 먼저 논문 속 예시를 보며 살펴보겠습니다.

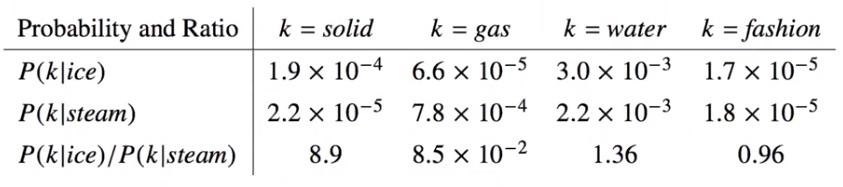
위의 표 중 첫 번째와 두 번째 row는 각각 ice과 steam이라는 단어가 주어졌을 때, k 단어가 나타날 확률을 나타냅니다. 예시에서는 k로 solid, gas, water, fashion이 주어져 있습니다. 마지막 세 번째 row에는 1, 2 row의 비로 표현됩니다. 각각의 값을 살펴보면 solid는 ice가 조건부 확률로 주어졌을 경우가 steam의 경우보다 더 등장확률이 높은 것을 알 수 있습니다. gas의 경우 solid와 반대로 나타나게 됩니다. 또한 ice, steam모두 관련이 있는 water / 모두 관련이 없는 fashion의 등장확률은 1, 2 행의 값이 비슷하게 나타나게 됩니다.

따라서 우리가 주목해야할 지점은 3번째 행입니다. 분자의 확률이 분모보다 더 클 경우, 즉 본 예시에서는 k 단어가 steam보다 ice에 더 연관이 많을 경우 해당 값은 1보다 큰 값으로 도출됩니다. (분모, 분자 차이가 클수록 값이 더 커져갑니다.) 반대의 경우에는 1보다 작은 값을 가지게 됩니다. 또한 3, 4번째 열과 같이 조건부 단어에 둘다 관련이 없거나 둘다 관련이 있는 경우(water, fashion) 1과 비슷한 값을 가지게 됩니다. 이 것이 바로 동시등장확률입니다.

GloVe 방법론은 Corpus전체에서 위와 같은 단어 간의 동시등장확률을 계산하여 단어들을 표현해내게 됩니다. 이에 따라 앞서 언급하였 듯, Corpus 전체의 Co-occurrence를 반영하면서도 단어 간의 관계를 표현해낼 수 있게 되는 것입니다.

Process of GloVe

그렇다면 동시등장확률을 활용하여 텍스트를 학습하는 목적함수(Objective function)를 알아보겠습니다. 동시등장확률을 이용한 목적함수를 수식으로 표현해보면 아래와 같습니다. (기본적인 notation은 위의 예시에서와 동일하게 사용)

ojf1

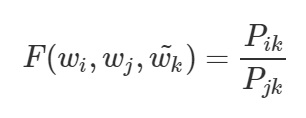
위 수식을 살펴보면, 어떠한 단어 벡터 K가 주어졌을 때 i, j 와의 관계에 대한 비를 구하는 함수 F를 의미합니다. 여기서 함수 F가 바로 우리가 구하고자 하는 목적함수가 될 것입니다. 위 수식을 차근차근 재표현해보도록 하겠습니다.

ojf2

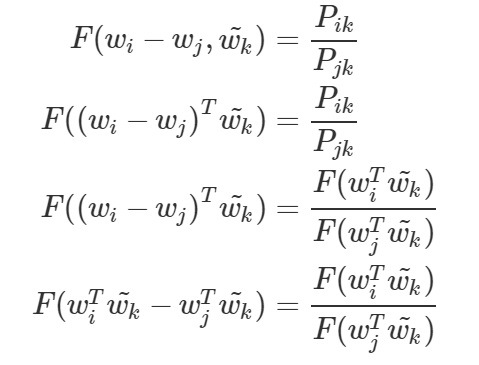
첫 번째 수식부터 살펴보도록 하겠습니다. 먼저 우리가 관심있는 i와 j 단어 벡터의 관계를 linear space에서 가장 쉽게 표현할 수 있는 방법인 차를 이용하여 함수를 구성합니다. 그 다음으로 scalar인 확률 값을 계산해주기 위하여 두 벡터를 내적한 값으로 표현하였습니다. 이 때, 두 번째 수식에서 우변에 나타난 확률 값의 비를 우리가 구하고자 하는 목적함수로 표현해주면 보다 손쉽게 단어 간의 관계를 파악할 수 있겠다는 아이디어로 i, j와 k를 내적한 값을 목적함 수에 넣어주는 형태로 표현을 하게 됩니다.

최종 수식을 만족하는 목적함수를 구하려면, 다음의 조건을 만족해야 합니다. 먼저 첫 째로, corpus상에서 i 단어 벡터는 언제든지 k 단어 벡터로 변환될 수 있어야 합니다. 또한 co-occurrence matrix가 symmetric하다는 것을 반영할 수 있어야 하며, 마지막 수식에서 나타난 것과 같이 함수 내 값의 차가 함수의 비로 표현되는 homomorphism 조건을 만족해야 합니다. 우리는 이 조건을 모두 만족하는 함수가 지수함수임을 알고 있습니다. 따라서 지수함수를 이용하여 위 식을 표현해보겠습니다.

obj3

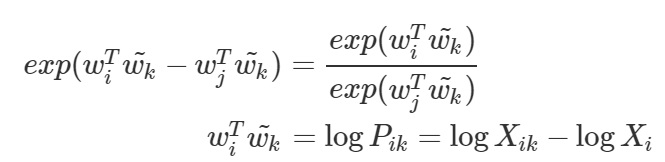
이 때, 두 번째 수식의 우변의 경우 위에서 언급한 것처럼 언제든 k와 i가 바뀔 수 있기 때문에 k와 i가 교체되더라도 바뀌지 않도록 수식을 로그가 아닌 상수 b로 재 표현해줍니다.

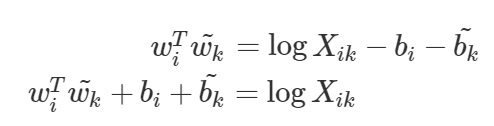
따라서 최종 수식에서 우변을 좌변으로 이항시키면 우리는 원하던 목적함수를 얻을 수 있습니다. 여기에 GloVe 연구팀은 조건식을 하나 더 추가해줍니다. 바로 대량으로 등장하는 단어들에 cap을 걸어주기 위함인데요. 만약 주어진 corpus 내에 굉장히 잦은 빈도로 출현하는 단어의 경우 우리의 목적 함수에서 noise가 될 수 있습니다. (제곱 term으로 빈도수가 높다면 목적함수의 값이 커질 것이므로) 따라서 단어의 빈도수가 아무리 많더라도 1에 cap을 걸어줌으로써 해당 단어에 대한 Overfitting을 방지하는 역할을 하는 f(X) term을 추가해서 곱해주게 됩니다.

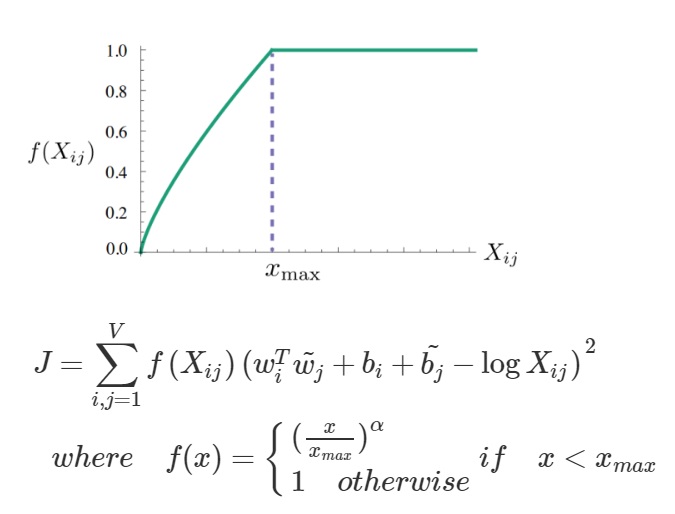
final

※ f(X) term의 알파의 경우 hyper parameter입니다. 논문에 따르면 simulation 결과, 알파가 3/4 일 때 가장 최상의 결과를 낸다고 주어져 있습니다.

### GloVe 실습