Narrow Confidence Interval for low N with small p
최근 Proportion 예측치에 대한 신뢰구간에 대해 생각해 볼 기회가 있었습니다. 어떤 완성된 제품의 판매 이후 기간 내 누적 불량률에 대해 예측하는 업무에 참여했는데요! 이 때 점 추청치도 물론 중요하지만, 구간 추청치에 대한 관심도 이에 못지 않은 것 같습니다. 범위로 표현되다보니 어느 정도의 규모의 불량률이 발생할 수 있는가에 대한 관심이라고 생각합니다.
이때 문제가 되었던 건 제품의 출시 초기, 즉, 누적 불량률 proportion에서 n이 적을 때의 신뢰 구간이 매우 크게 벌어진다는 것입니다. 따라서 예측치로서의 가치가 퇴색되는 문제가 있습니다. 이에 초기 불량률 예측에서도 나름대로 적정한 범위를 갖는 신뢰구간을 제시하기 위해 고민해본 결과를 정리해보겠습니다.
Problem setting
앞 서 간단하게 설명한 문제를 구체적인 토이 데이터를 가지고 정의해보겠습니다. (본 포스팅에서 제시되는 데이터는 실제 데이터가 아니며 실제 데이터의 특성을 반영하여 임의로 생성된 데이터입니다.)
| timestamp | x_cumulative | n_cumulative | proportion |
|---|---|---|---|
| 21-04-01 0시 | 4 | 37 | 0.11 |
| 21-04-01 6시 | 7 | 76 | 0.09 |
| 21-04-01 12시 | 11 | 123 | 0.09 |
| 21-04-01 18시 | 15 | 168 | 0.08 |
| 21-04-02 0시 | 20 | 216 | 0.09 |
| 21-04-02 6시 | 25 | 264 | 0.10 |
| … | … | … | … |
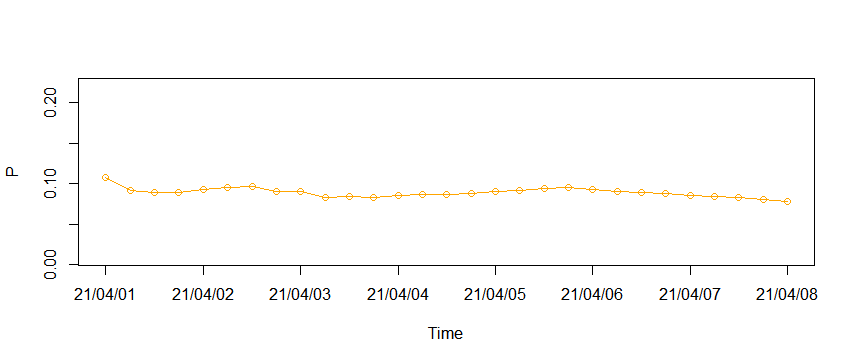
위 데이터는 2021년 4월 1일부터 4월 8일까지 1주일간 6시간에 한번씩 제품의 누적 불량률 예측치를 기록한 것입니다. x는 불량이 일어난 제품의 수를 뜻하고 n은 출시된 전체 제품 수입니다. proportion은 이들의 비율로서 불량률에 해당하며 테이블에 기록된 내용들을 전부 어떤 모델로 예측했다고 가정해보겠습니다.
예측된 누적 불량률의 신뢰구간을 구해보겠습니다. 우선 가장 기본인 정규 근사를 이용한 비율 신뢰구간을 적용해보겠습니다.
\[CI_{normal} = \hat{p} \pm z\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\]
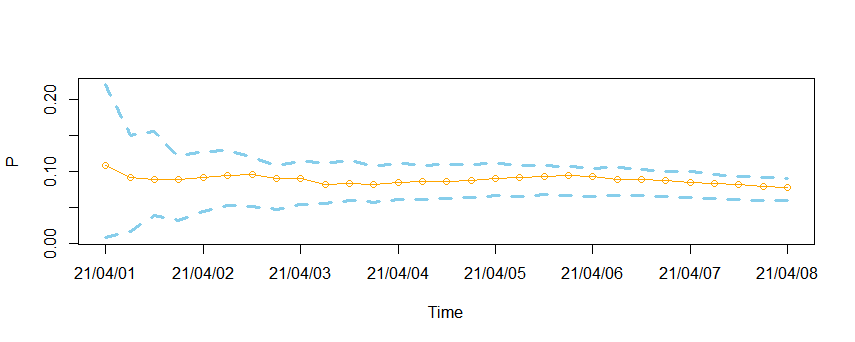
서두에서 말씀드린 것처럼 4월 1일의 초기 예측 불량률에 대한 구간이 위아래로 크게 벌어진 것을 확인할 수 있습니다. 이후 4월 3일 경부터 n이 누적되어 커지면서 구간이 안정을 찾는 것을 확인할 수 있네요! 저는 저 초기 불량률에 대한 신뢰구간을 적정하게 줄여서 활용 가능성을 높이고 싶었습니다.
그래서 생각한 것이 예측된 값의 특성을 반영해주면 좋겠다는 것이었습니다. 불량률의 모습을 살펴보시면 p가 작음을 확인할 수 있습니다. 불량률이나 연체율 등의 나쁜 비율들에서 흔히 나타나는 imbalance 특성인데요! 이를 반영하여 구간을 도출하면 좀 더 개선된 구간이 도출될 수 있지 않을까 생각했습니다.
여기까지 진행되었을 때 떠올랐던 것이 바로 Bayesian Credible Interval이었습니다. Bayesian Interval은 Bayesian inference를 통해서 posterior의 분포를 이용하여 p의 interval을 계산해주는 방법입니다. 이 때 prior를 통해서 불량률의 사전 정보를 반영해줄 수 있으니 low p에 대한 정보를 반영할 수 있다고 생각했습니다!
Jeffrey’s Prior
우선 Bayesian Interval 중에서 가장 유명한 Jeffrey’s prior부터 적용해보겠습니다. Jeffrey prior는 \(Beta(1/2, 1/2)\)을 prior로 주는 것인데요. Beta분포 자체가 0~1 사이의 proportion에 대한 정보를 담고 있는 분포니까 prior로서 적합합니다.
(* 사실 Bayesian Credible Interval은 Confidence Interval과 살짝 다른 개념이긴 하지만 대체로 비슷하므로 그냥 사용하겠습니닷)
(* low p를 반영해준다고 하고 jeffrey를 먼저 적용하는 건 말이 안되지만 (뒤에서 설명) 비교를 위해서 먼저 적용해보았습니닷)
Interval을 구하는 수식과 실제 계산 결과는 다음과 같습니다.
\[\begin{gathered} CI_{jeffrey} = [Beta(\alpha/2; x+1/2, n-x+1/2),Beta(1-\alpha/2; x+1/2, n-x+1/2)] \end{gathered}\]
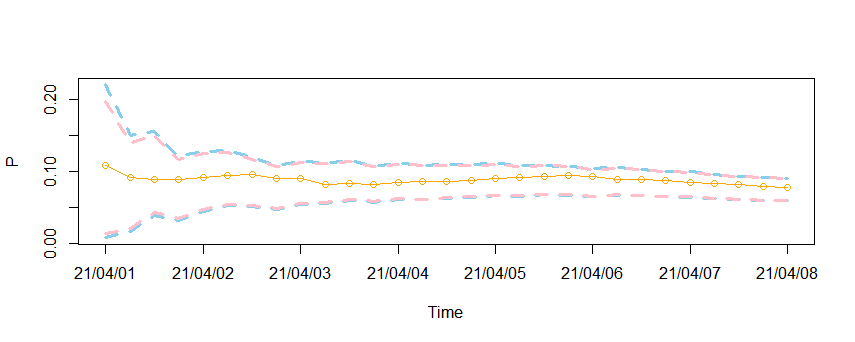
분홍색으로 구해진 것이 jeffrey prior를 통해 구한 Interval인데요. 기존 신뢰구간에 비해 살짝 작아지긴 했지만 여전히 초기 불량률에 대한 구간이 벌어져있네요 ㅠㅠ 제가 생각한 Jeffrey prior의 문제는 다음과 같습니다.
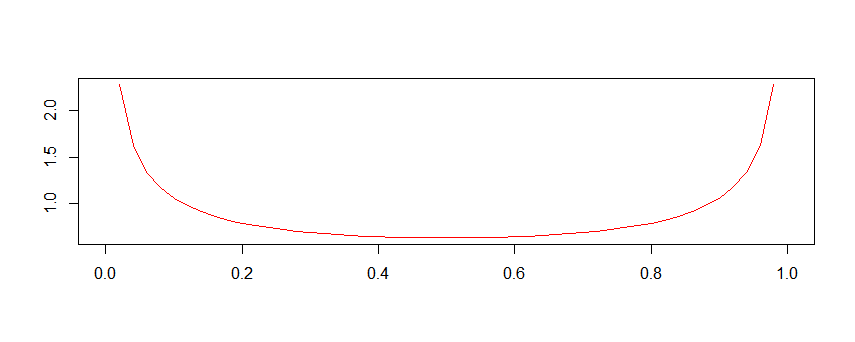
Jeffrey prior의 모습입니다. Low p에 대한 density도 높지만 Large p에 대한 density도 높은 것을 확인할 수 있습니다. 저희의 불량률 데이터는 large p가 나올 수 없는(정확히는 나오면 안되는 ^^;;) 형태이기 때문에 prior의 형태를 수정할 필요가 있어보입니다!
Modified Prior
그래서 prior로 사용되고 있는 Beta 분포에서 parameter를 바꿔줬습니다. Jeffrey의 0.5, 0.5가 아니라 0.05, 35를 parameter로 갖는 beta 분포를 prior로 사용해보겠습니다.
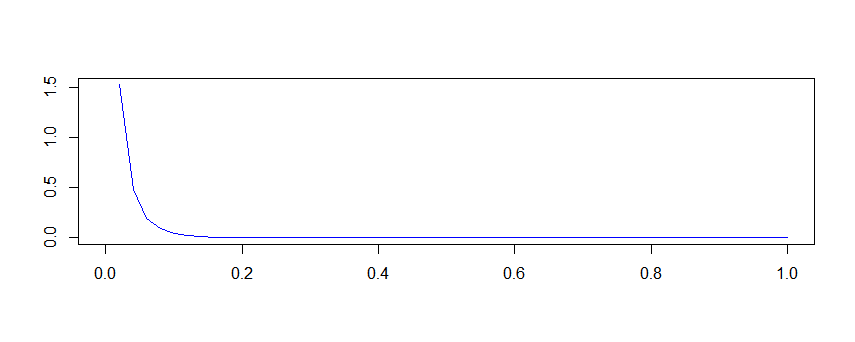
수정된 prior의 모습은 위와 같습니다. small p에 대한 density만이 높게 잡히는 형태로 되어있음을 확인할 수 있습니다! 이러한 사전 정보를 가지고 Interval을 계산하면 수식이 다음과 같이 변경됩니다.
\[\begin{gathered} CI_{mod} = [Beta(\alpha/2; x+0.05, n-x+35),Beta(1-\alpha/2; x+0.05, n-x+35)] \end{gathered}\]이제 준비는 끝났습니다! 계산된 Interval의 결과를 보시죠!
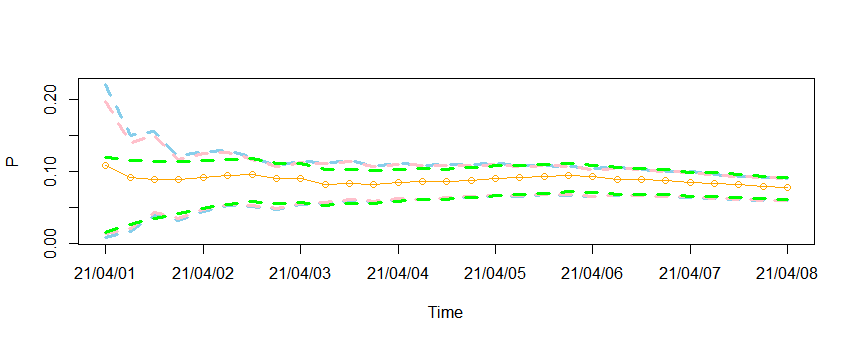
초록색 선으로 구해진 것이 modified Interval입니다. 기대 했던대로 다른 구간들에 비해 초기 불량률에 대해 작은 구간으로 define되었음을 확인할 수 있습니다!
Limitation
간단하게 small p에 대한 사전 정보를 반영하여 low n의 신뢰 구간을 좁히는 방법을 생각해보았습니다. 이 방법의 개선해야할 부분, 더 생각해볼 지점은 다음과 같습니다.
- prior의 parameter 세팅
modified Interval의 prior는 \(Beta(0.05, 35)\)로 되어있습니다. 이 때 0.05, 35는 어떻게 정해졌을까요? 네, 제가 임의로 정했습니다 ㅎㅎ 하지만 모든 데이터에 대해 임의로 사람이 지정해줄 수는 없는 노릇이니, 이 부분을 결정하는 logic이 필요해보입니다.
- 굳이 신뢰구간을 좁혀야 하는가?
“신뢰 구간”이라는 것 자체가 n이 커지면 자연히 좁아지고 n이 작으면 넓어지는 것이 당연합니다. 이는 통계적 추론에서 수반되는 불확실성의 반영이기도 합니다. 따라서 n이 작은 기간에 신뢰 구간을 좁히는 것이 필요한 작업인지에 대해서는 업무 내에서의 활용 방안, 분석의 목적에 맞추어 판단해야 될 부분으로 보입니다.
결론적으로 이 방법론은 무조건적인 적용이 아니라 (모든 것이 그렇지만) 때와 장소에 따라서 분석자가 적절히 적용하여 활용하는 것이 가장 좋겠다는 의견입니다! ㅎㅎ
